Hitskin.comThis is a Hitskin.com skin preview
Install the skin • Return to the skin page
Home
Latest imagesa challenging algebra/geometry problem
+3
Marathadi-Saamiyaar
Bittu
MaxEntropy_Man
7 posters
Page 1 of 1
a challenging algebra/geometry problem
by MaxEntropy_Man Thu Sep 27, 2012 9:10 am
let triangle ABC with sides a, b, and c have perimeter 2. prove that:
a^2+b^2+c^2+2abc < 2
a^2+b^2+c^2+2abc < 2
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by Guest Thu Sep 27, 2012 11:17 am
Here's a solution from the son-dad team.
a^2+b^2+c^2+2bc = (a+b)^2-2ab+c^2+2abc = (2-c)^2+c^2-2ab(1-c). The last step uses the fact that (a+b) = 2-c.
Without loss of generality, we assume that c is the largest side and b is the second largest. Note that 2/3<=c<=1 because of the triangle inequality and the given bound on the perimeter.
Now imagine that c is fixed. To maximize the above expression, we need to find the minimum value of ab as a function of c. Since (a+b) = 2-c, in order to minimize ab, we need to make a and b as unequal as possible. Recall also that b must be less than or equal to c. So the minimum value of ab is realized when b=c and a=2(1-c). Therefore ab>=2c(1-c).
Using this fact in the expression above, we get (2-c)^2+c^2-2ab(1-c)<=(2-c)^2+c^2-4c(1-c)^2 which simplifies to -4c^3+10c^2-8c+4.
Using calculus, it is easy to see that the maximum value of this expression in the range 2/3<=c<=1 occurs when c=1 and the maximum value is 2.
a^2+b^2+c^2+2bc = (a+b)^2-2ab+c^2+2abc = (2-c)^2+c^2-2ab(1-c). The last step uses the fact that (a+b) = 2-c.
Without loss of generality, we assume that c is the largest side and b is the second largest. Note that 2/3<=c<=1 because of the triangle inequality and the given bound on the perimeter.
Now imagine that c is fixed. To maximize the above expression, we need to find the minimum value of ab as a function of c. Since (a+b) = 2-c, in order to minimize ab, we need to make a and b as unequal as possible. Recall also that b must be less than or equal to c. So the minimum value of ab is realized when b=c and a=2(1-c). Therefore ab>=2c(1-c).
Using this fact in the expression above, we get (2-c)^2+c^2-2ab(1-c)<=(2-c)^2+c^2-4c(1-c)^2 which simplifies to -4c^3+10c^2-8c+4.
Using calculus, it is easy to see that the maximum value of this expression in the range 2/3<=c<=1 occurs when c=1 and the maximum value is 2.
Guest- Guest
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Thu Sep 27, 2012 11:50 am
note that the inequality is not a less than or equal to, but less than.
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Thu Sep 27, 2012 12:03 pm
further to what i wrote above, note that if we set c=1 (per f&s's solution), then b necessarily has to be equal to 1-a. when you then substitute c=1, and b = 1-a, the LHS of the given inequality simplifies to 2 (and is independent of a). this would imply that as long as c=1, all positive values of a and b satisfying a+b=1 mazimize the given expression which is always equal to 2 (so long as c=1). clearly that cannot be.
eta: it can be solved by multivariable calculus using a very particular technique. that's what i did. however, there is a completely algebraic solution which eschews calculus (not my solution), which is difficult but incredibly beautiful. the calculus method is straightforward if you know this particular method. i know it because i use it on and off in my work in connection with other problems. it's a bit of a brute force method. let me know if f&s need the name of the method which may also serve as a strong hint.
eta: it can be solved by multivariable calculus using a very particular technique. that's what i did. however, there is a completely algebraic solution which eschews calculus (not my solution), which is difficult but incredibly beautiful. the calculus method is straightforward if you know this particular method. i know it because i use it on and off in my work in connection with other problems. it's a bit of a brute force method. let me know if f&s need the name of the method which may also serve as a strong hint.
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by Guest Thu Sep 27, 2012 12:20 pm
Are you referring to the method of Lagrange multipliers? It would be nice to see both your calculus based and algebraic approaches.
I see that you are ruling out degenerate triangles, in which all three vertices are colinear, which is reasonable.
I see that you are ruling out degenerate triangles, in which all three vertices are colinear, which is reasonable.
Guest- Guest
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Thu Sep 27, 2012 12:21 pm
yes. lagrange multipliers. i will post both solutions if there are no other takers by 8 PM EDT.
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by Bittu Thu Sep 27, 2012 3:29 pm
Threads like this make me acutely aware of my shitty education and I start feeling quite shitty overall.
Bittu- Posts : 1151
Join date : 2011-08-19
Re: a challenging algebra/geometry problem
by Marathadi-Saamiyaar Thu Sep 27, 2012 3:51 pm
Bittu wrote:Threads like this make me acutely aware of my shitty education and I start feeling quite shitty overall.
I feel your pain. At least, you got an education of some sort; but, I did not even get that.
Marathadi-Saamiyaar- Posts : 17675
Join date : 2011-04-30
Age : 110
Re: a challenging algebra/geometry problem
by PavanP_Nahata_Plus_MAIyer Thu Sep 27, 2012 4:54 pm
We want to prove
.
Multiply both sides by 4:
.
Since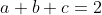
, we can make (2) homogenous of degree three by writing it as
.
Multiply out the brackets in (3) and rearrange it a bit, and you will get
.
So far, the argument is reversible, so if we can prove (4) then (1) will also hold.
We are told that
, 
and 
. Therefore
.
Multiply out the brackets in (5), rearrange it a bit, and you get exactly the inequality (4), as wanted.
Google helps
Multiply both sides by 4:
Since
Multiply out the brackets in (3) and rearrange it a bit, and you will get
So far, the argument is reversible, so if we can prove (4) then (1) will also hold.
We are told that
Multiply out the brackets in (5), rearrange it a bit, and you get exactly the inequality (4), as wanted.
Google helps
PavanP_Nahata_Plus_MAIyer- Posts : 10
Join date : 2012-09-27
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Thu Sep 27, 2012 5:54 pm
PPNIyer -- yes thanks for saving me the typing. that is indeed the algebraic solution involving no calculus. it is very ingenious. the trick is in homogenizing the inequality which also involves the incredibly clever device of replacing 2 with a+b+c! that would have never occurred to me in a million years.
the brute force method of lagrange multipliers is what i used. here is how the solution proceeds:
set,
f = a^2+b^2+c^2+2abc
f has to be maximized subject to the constraint that,
g = a+b+c = 2
we now have three equations
D[f,a]+ alpha D[g,a]=0
D[f,b]+ alpha D[g,b]=0
D[f,c]+ alpha D[g,c]=0
in the above alpha is the undetermined multiplier and terms like D[f,a] mean partial derivative of f wrt a and so on. the above three equations along with the constraint equation give four equations in four unknowns, namely, a, b,c, and alpha which can be solved with a bit of algebra (i cheated and used mathematica).
the results give,
alpha = -20/9 and a=b=c=2/3
substituting these back in f, one gets,
fmax = 52/27 which is < 2.
the brute force method of lagrange multipliers is what i used. here is how the solution proceeds:
set,
f = a^2+b^2+c^2+2abc
f has to be maximized subject to the constraint that,
g = a+b+c = 2
we now have three equations
D[f,a]+ alpha D[g,a]=0
D[f,b]+ alpha D[g,b]=0
D[f,c]+ alpha D[g,c]=0
in the above alpha is the undetermined multiplier and terms like D[f,a] mean partial derivative of f wrt a and so on. the above three equations along with the constraint equation give four equations in four unknowns, namely, a, b,c, and alpha which can be solved with a bit of algebra (i cheated and used mathematica).
the results give,
alpha = -20/9 and a=b=c=2/3
substituting these back in f, one gets,
fmax = 52/27 which is < 2.
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Thu Sep 27, 2012 6:04 pm
the one additional thing that my solution reveals is the symmetry in the problem. the LHS of the given inequality is symmetric in a, b & c. so it is not a huge surprise that the set of values of a, b, and c that maximizes the given expression turn out to be equal.
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by Guest Thu Sep 27, 2012 10:02 pm
Feedback from f&s:
The algebraic solution is elegant but there is a bug in the Lagrange multipliers solution. The maximum value of the expression is not attained when a=b=c=2/3. To see this, consider a triangle with side lengths 1-eps, 1-eps, 2eps where eps is an arbitrary small positive number. Such a triangle clearly exists. The quantity a^2+b^2+c^2+2abc for this triangle approaches 2 as eps->0.
In light of this observation, the solution we gave is correct. (If you exclude degenerate triangles, then the expression cannot actually equal 2 but only come as close to 2 as you please.)
Your Lagrange multipliers solution perhaps minimizes the expression? If yes, a variant of the original problem would be to show that the expression lies between 52/27 and 2, for any triangle.
The algebraic solution is elegant but there is a bug in the Lagrange multipliers solution. The maximum value of the expression is not attained when a=b=c=2/3. To see this, consider a triangle with side lengths 1-eps, 1-eps, 2eps where eps is an arbitrary small positive number. Such a triangle clearly exists. The quantity a^2+b^2+c^2+2abc for this triangle approaches 2 as eps->0.
In light of this observation, the solution we gave is correct. (If you exclude degenerate triangles, then the expression cannot actually equal 2 but only come as close to 2 as you please.)
Your Lagrange multipliers solution perhaps minimizes the expression? If yes, a variant of the original problem would be to show that the expression lies between 52/27 and 2, for any triangle.
Guest- Guest
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Thu Sep 27, 2012 10:55 pm
hmmm...i see what they mean. i also ran a one line code in mathematica for the constrained maximum problem using FindMaximum and it found the same solution i did, but yet your boys have a point. i seem to have hit a snag. mathematica also gave me the same result when i did a FindMinimum! i wonder if that's a saddle point rather than a maximum. need to explore some more. in light of this, i must accept f&s's original heuristic method.
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by aanjaneya Thu Sep 27, 2012 11:08 pm
That is correct.
The said expression does not have a 'maximum'. It only has a 'supremum', whose value is 2, and you can come arbitrarily close to 2 from below, but never achieve it, if we exclude the degenerate case.
A simpler example of such behavior:
Maximize f(X) = X, s.t. X < 2.
f(X) has no maximum, it only has a supremum, whose value is 2.
For the Lagrangian associated with the above problem, the first order conditions only let you characterize a stationary point.
To further qualify this stationary point, one needs to look at higher order terms (in the sense of a Taylor series expansion, around the stationary point), beginning with the Hessian of the Lagrangian.
So the argument based on just computing the stationary point and claiming the strict inequality is indeed mathematically flawed.
In any case, this problem had me stumped. But enjoyed the dismissal nevertheless.
The said expression does not have a 'maximum'. It only has a 'supremum', whose value is 2, and you can come arbitrarily close to 2 from below, but never achieve it, if we exclude the degenerate case.
A simpler example of such behavior:
Maximize f(X) = X, s.t. X < 2.
f(X) has no maximum, it only has a supremum, whose value is 2.
For the Lagrangian associated with the above problem, the first order conditions only let you characterize a stationary point.
To further qualify this stationary point, one needs to look at higher order terms (in the sense of a Taylor series expansion, around the stationary point), beginning with the Hessian of the Lagrangian.
So the argument based on just computing the stationary point and claiming the strict inequality is indeed mathematically flawed.
In any case, this problem had me stumped. But enjoyed the dismissal nevertheless.
aanjaneya- Posts : 15
Join date : 2012-09-17
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Thu Sep 27, 2012 11:12 pm
aanjaneya wrote:
To further qualify this stationary point, one needs to look at higher order terms (in the sense of a Taylor series expansion, around the stationary point), beginning with the Hessian of the Lagrangian.
i was just beginning to look at that! although i haven't done it yet, i suspect it's a saddle point since mathematica gave me the same solution for FindMaximum and FindMinimum. this is a good cautionary tale for me as i am about to start looking at applications of this method to solve some problems in classical and statistical thermodynamics.
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by Guest Sun Sep 30, 2012 4:23 pm
just a messenger, pliss not to shoot
http://forums.sulekha.com/forums/wo-men/solution-to-max-s-math-problem-let-triangle-abc-with-sides-a-b-and-c-have-perimeter-2-prove-that-201808.htm#201808
http://forums.sulekha.com/forums/wo-men/another-solution-to-max-s-math-problem-201810.htm
http://forums.sulekha.com/forums/wo-men/solution-to-max-s-math-problem-let-triangle-abc-with-sides-a-b-and-c-have-perimeter-2-prove-that-201808.htm#201808
http://forums.sulekha.com/forums/wo-men/another-solution-to-max-s-math-problem-201810.htm
Guest- Guest
Re: a challenging algebra/geometry problem
by Idéfix Sun Sep 30, 2012 5:38 pm
Sevaji, it is time to talk to Max directly. We know you visit us, so might as well start solving problems right here. At least your solutions will get formatted correctly here.
Idéfix- Posts : 8808
Join date : 2012-04-26
Location : Berkeley, CA
Re: a challenging algebra/geometry problem
by Guest Sun Sep 30, 2012 5:40 pm
panini press wrote:Sevaji, it is time to talk to Max directly. We know you visit us, so might as well start solving problems right here. At least your solutions will get formatted correctly here.
+1
Guest- Guest
Re: a challenging algebra/geometry problem
by Kris Sun Sep 30, 2012 8:09 pm
http://forums.sulekha.com/forums/wo-men/another-solution-to-max-s-math-problem-201810.htm[/quote[/url]]Natalia Romanova wrote:just a messenger, pliss not to shoot
http://forums.sulekha.com/forums/wo-men/solution-to-max-s-math-problem-let-triangle-abc-with-sides-a-b-and-c-have-perimeter-2-prove-that-201808.htm#201808
[url=http://forums.sulekha.com/forums/wo-men/another-solution-to-max-s-math-problem-201810.htm
>>>I would like for Seva to post it here too. I started playing around with it along the same lines, but hit a brick wall. My knowledge about the properties of triangles was not that great to begin with. Still curious to see how Seva did this algebraically.
Kris- Posts : 5461
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by Guest Mon Oct 01, 2012 3:52 am
seva, what is wrong with you? on one hand you say you are old and weary and are cutting down your online time. on the other hand you are reading posts here with a fine-tooth comb and even taking the pain to respond to our comments here by posting there, including to the comments i made here on your language-migration blog. such contradictory behaviour does not behoove a senior, committed, highly educated and learned participant as you (your proof above is elegant! max and bw complicate things). resolve the internal contradictions and act normal for petes sake! so, come, or correspond, gentle seva.
Guest- Guest
Re: a challenging algebra/geometry problem
by Guest Mon Oct 01, 2012 4:20 am
seva, Y being negative is right but where's the proof?
Guest- Guest
Re: a challenging algebra/geometry problem
by Guest Mon Oct 01, 2012 8:14 am
Huzefa Kapasi wrote: (your proof above is elegant! max and bw complicate things). resolve the internal contradictions and act normal for petes sake! so, come, or correspond, gentle seva.
why is the f&s method complicated? it is very simple with some basic application of calculus, that's all.
seva's proof is very nice indeed.
Guest- Guest
Re: a challenging algebra/geometry problem
by Guest Mon Oct 01, 2012 8:31 am
i got scared by lagrange series and did not read further but i get your point. f&s solution is basic calculus. lagrange is max's solution and not necessary per se. algebraic substitution (pnpm) requires pyrotechnics. i forwarded this problem to my older this morning. he will take a crack tonight after his classes are over. only after that will i go into the f&s solution to understand and help older (if he does not succeed on his own).
Guest- Guest
Re: a challenging algebra/geometry problem
by Guest Mon Oct 01, 2012 1:16 pm
older just called me. he laughed at my story (it is not a story!) and explained that the girls hostel was a few kms away and that google maps was not always accurate. he also said that he was unable to solve this problem. he and his friends then discussed with chacha, their hostel security guard, who is the last word in math and chacha explained that lagrange series was not in their first year curriculum and that this math problem was not germane to their engineering discipline/major. case closed. older also said that it was good that karnataka had stopped giving water to TN. BJP bandhs had postponed their exams.
Guest- Guest
Re: a challenging algebra/geometry problem
by Guest Mon Oct 01, 2012 3:10 pm
Huzefa Kapasi wrote:older just called me. he laughed at my story (it is not a story!) and explained that the girls hostel was a few kms away and that google maps was not always accurate. he also said that he was unable to solve this problem. he and his friends then discussed with chacha, their hostel security guard, who is the last word in math and chacha explained that lagrange series was not in their first year curriculum and that this math problem was not germane to their engineering discipline/major. case closed. older also said that it was good that karnataka had stopped giving water to TN. BJP bandhs had postponed their exams.
LOL @ curriculum and college bandh happiness. Yep he is from my engineering category. Chabuk padegi tab hee daudenge types. Soon he will learn the great arts of mass copying assignments and topo-something. Overall, totally proud of him. He gonna come out totally resourceful.
Guest- Guest
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Mon Oct 01, 2012 5:16 pm
i'm glad i created this thread. although i was dead wrong with my reasoning using lagrange multipliers for this problem, i went back and cracked a real publishable problem that had been bugging me for six years that i had put away a while ago. it finally yielded this past weekend after i applied all the tricks i used on this one to no avail. to the folks who participated, a huge thanks! riding a minor emotional high.
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by Guest Mon Oct 01, 2012 11:28 pm
LOL!Natalia Romanova wrote:Yep he is from my engineering category. Chabuk padegi tab hee daudenge types. Soon he will learn the great arts of mass copying assignments and topo-something. Overall, totally proud of him. He gonna come out totally resourceful.
yup, good job Il Professore. i enjoyed this thread and your obsessive absorption with solutions to the problem. enjoy the high -- you deserve it.MaxEntropy_Man wrote:i'm glad i created this thread. although i was dead wrong with my reasoning using lagrange multipliers for this problem, i went back and cracked a real publishable problem that had been bugging me for six years that i had put away a while ago. it finally yielded this past weekend after i applied all the tricks i used on this one to no avail. to the folks who participated, a huge thanks! riding a minor emotional high.
Guest- Guest
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Tue Oct 02, 2012 9:13 am
Natalia Romanova wrote:
Yep he is from my engineering category. Chabuk padegi tab hee daudenge types. Soon he will learn the great arts of mass copying assignments and topo-something.
hello bollywood queen. what do the above sentences mean? what is an "engineering category"? and what does the sentence starting with chabuk mean? and what does it mean to topo-something?
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by Guest Tue Oct 02, 2012 9:17 am
MaxEntropy_Man wrote:Natalia Romanova wrote:
Yep he is from my engineering category. Chabuk padegi tab hee daudenge types. Soon he will learn the great arts of mass copying assignments and topo-something.
hello bollywood queen. what do the above sentences mean? what is an "engineering category"? and what does the sentence starting with chabuk mean? and what does it mean to topo-something?
blues king, HK lol'ed on my post. that's enough for now. will explain the rest later.
Guest- Guest
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Tue Oct 02, 2012 9:21 am
i put that sentence in google translator and it translated to english as,
"only then will lash gate...".
"only then will lash gate...".
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by Guest Tue Oct 02, 2012 9:23 am
MaxEntropy_Man wrote:i put that sentence in google translator and it translated to english as,
"only then will lash gate...".
it's saying we are like horses, who run only when prompted/lashed. I stole these lines from my cousin.
Guest- Guest
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Tue Oct 02, 2012 9:25 am
Natalia Romanova wrote:MaxEntropy_Man wrote:i put that sentence in google translator and it translated to english as,
"only then will lash gate...".
it's saying we are like horses, who run only when prompted/lashed. I stole these lines from my cousin.
ok thanks.
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Re: a challenging algebra/geometry problem
by Guest Tue Oct 02, 2012 9:32 am
MaxEntropy_Man wrote:i put that sentence in google translator and it translated to english as,
"only then will lash gate...".
how did you put it in the google translator? did you have to retype it in devanagari?
Guest- Guest
Re: a challenging algebra/geometry problem
by MaxEntropy_Man Tue Oct 02, 2012 9:34 am
Huzefa Kapasi wrote:MaxEntropy_Man wrote:i put that sentence in google translator and it translated to english as,
"only then will lash gate...".
no it takes input in english and converts to devanagari.
MaxEntropy_Man- Posts : 14702
Join date : 2011-04-28
Similar topics» a ninth grade algebra problem
» a reasonably challenging math problem
» Is Algebra Necessary?
» How Muslims Did Not Invent Algebra
» challenging times for Obama
» a reasonably challenging math problem
» Is Algebra Necessary?
» How Muslims Did Not Invent Algebra
» challenging times for Obama
Page 1 of 1
Permissions in this forum:
You cannot reply to topics in this forum